pbrt 是一個基於物理的 ray-tracing libarary，他可以拿來產生接近現實的真實場景，據說 IKEA 的型錄都是用類似方法產生的，而不是真的把產品擺出來拍照。 哈哈

據說 IKEA 型錄的圖都是渲染出來的<sup>[1]</sup> 據說 IKEA 型錄的圖都是渲染出來的[1]

關於 pbrt 與 ray-tracing

Ray-tracing 說穿了就是在模擬自然界光線的運作，我們之所以看的到東西，其實就是因為光線打到物體並反射到我們眼睛，這也是為甚麼在無光的地方會伸手不見五指(因為沒有任何光打到手指並反射到眼中)。
至於電腦要怎麼模擬這件事，大致來說是光線從光源出發，途中遇到障礙物就要算交點，有交點就要根據材質特性反射，反射之後就是一條新的光線，就繼續做交點測試直到進到眼睛中(或直到能量遞減完畢)。可以看出，ray-tracing 最重要的大概就是與物件算交點了，因為 ray 會一直做交點測試，所以與物件的交點測試必須要夠快才行，不然就會算到天荒地老….

pbrt 除了最基本的 triangleMesh 以外，還實作很多其他一些常見的 shape(球體、圓柱體、圓形、heightfield…)，這其實是拿來給 api 使用的，一般人可以寫 pbrt 專用的描述檔來描述一個場景中的物體、光源等等，再藉由 pbrt 的程式來渲染出整張影像。

pbrt 中的各種 shape，有些是會先轉成 triangleMesh(對三角形求交點應該是圖學中最基礎的了，如果原本物件太複雜通常就會先把它拆成三角形組合再來算)；而有些是有實作對 shape 交點測試的。由於把物件轉成 triangleMesh 其實就硬是多一個步驟了啊，如果可以與 shape 直接求交點，那速度上當然會大躍進~

實作 heightfield 交點測試

Heightfield 其實就是平面但是有高低差，也就是說，對每個而言只會有一個值。算是個滿單純的 shape。
Heightfield 也是原本就有實作的一種 shape，是直接用 Refine() 來把形狀轉為 triangleMesh 再做交點測試的。

如果能夠跳過三角化而直接與 heightfield 做交點測試，可能可以比較快喔？
參考一下別的 shape，包含球體、圓柱體等實作的交點測試的方法都是在幾何意義上直接求交點，也就是算數學求解哈哈
但 heightfield 似乎是沒辦法從幾何意義上直接解了，需要用更暴力的方法

這邊我是使用 DDA(digital differential analyzer) 來做交點測試，這東西其實原本是拿來畫線的演算法，因為實際上的線是連續的，但是呈現在電腦上卻必須以 pixel 為單位呈現。而這邊與 heightfield 的交點測試就是將 DDA 擴展至三維空間中(多了Z軸)。

2D-DDA 邏輯。<sup>[2]</sup> 2D-DDA 邏輯。[2]

可以看到其實可以在一開始就算出x, y要走多少會到下一個 pixel，這些都是定值，也讓遍歷整個 Pixel-Grid 變得很容易，而 3D-DDA 就只是再加入 z 軸的資訊，並且每一個 pixel 變成 voxel。
3D-DDA 這樣的方式其實在 pbrt 裡面已有實作，是來作為加速結構用途，但是由於 heightfield 本身特性(對每個而言只會有一個值)，我們可以讓 Voxel 的高度等於 heightfield 的高度，如此一來就可以讓3D結構的 heightfield 套用 2D-DDA 了！耶~~~

建好 DDA 需要的資訊後，接下來就是要實作 Ray 交點測試了，在遍歷 Voxel 的過程中，需要針對這個 Voxel 做交點測試，如果有交點就結束了；沒有就到下個 Voxel。
而關於每個 Voxel 的交點測試其實也是滿單純的，在設計 DDA 的結構時，除了讓 Voxel 高等於 heightfield 高，可以變成 2D-DDA 以外，讓 Voxel 的寬等於一個單位的 x 及 y 也是有很大的好處的，如下圖:

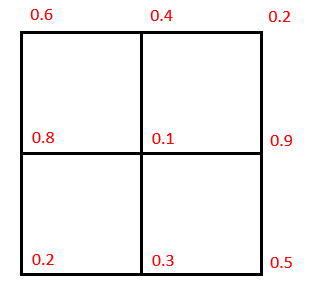從正上方看下來的 heightfield 樣子，數值為對應 z 值。讓 Voxel 寬度等於一格寬有好處。 從正上方看下來的 heightfield 樣子，數值為對應 z 值。讓 Voxel 寬度等於一格寬有好處。

依據這樣的設計，每次在做 Voxel 交點測試時，可以知道這 Voxel 中就是包含兩個三角形；也就是說分別對這兩個三角形做交點測試就好了~~

根據這樣的算法，就可以得出與原本直接三角化的做法一模一樣的結果:

用直接求交點的方式取代原本先做三角化的方法。 用直接求交點的方式取代原本先做三角化的方法。

平滑化

看看上圖的結果，看得出都是一面一面的三角形面，這是因為同一個面上所有點都是一樣的法向量，所以反射角度也都一樣，自然就成這副德性。
如果要做平滑化的話就必須內插三角形內部的點的法向量，使得三角面反射光會看起來滑順一點。

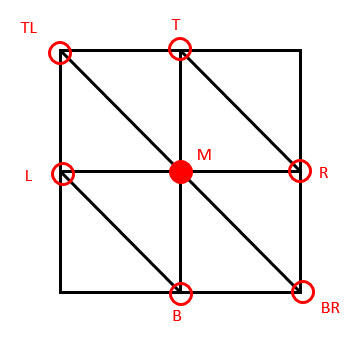三角化後每個點 M 都有六個鄰居。 三角化後每個點 M 都有六個鄰居。

這邊我是直接平均法向量來達成這樣的效果，由於三角化之後每個點會有六個鄰居；
點 M 的鄰居有 TL、T、R、BR、B、L 六點，點 M 的法向量可以藉由任意兩向量外積得出。

那我就平均一下六個法向量來當作真正的法向量，以 M 為原點，可算出平均法向量為:

這樣子改進後，就可以讓結果變這樣:

平滑化的結果 平滑化的結果

浮點數精度問題(10/22 更新)

做完平滑化之後，感覺海好像怪怪的歐….
一開始其實我還沒察覺，過這麼久才發現這問題…

很顯然只有海有這樣的問題，八成是因為海的值差距太小，計算法向量時的誤差。
用這樣的思維去追查程式後，發現我原本在算六個法向量總和後有做 Normalize(sumOfNormals)，這步驟造成值起伏太小的海的計算誤差….
把 Normalize() 拔掉之後就正常了～

修正浮點數精度問題後的結果 修正浮點數精度問題後的結果

加速

很可惜的是我做完以後，速度沒有想像中的快速，反而比原本的還慢了兩倍以上….嗚嗚嗚….
稍微看看別的 shape 的交點測試，其實有很多時候會先跟 Bbox(Bounding Box) 做測試，因為與 Bbox 交點是容易很多的，如果與 Bbox 無交點就也不用繼續做下去了。
在 Voxel 交點測試中，也應當先與整個 Voxel 做測試，確定有交點再去試裡面的兩個三角形，這樣就可以省下很大量的做白工。

但這樣做完還是不夠好，所以我利用 CPU profiling 來測試我的程式的瓶頸到底在哪裡….
利用這樣的檢測，我陸續做了幾次優化:

原因及改善方法Intersect()與未最佳化時比較
未最佳化。90,274100.0%
發現 ObjectBound() 很慢，改在 Heightfield construction 時就先存 minZ, maxZ。82,73191.6%
發現在算 Voxel BBox 使用的 Bbox(Union(Bbox, Bbox)) 超爆慢，改用 Bbox(Point, Point)。53,40859.1%
發現有不必要的坐標系轉換，由於在 Voxel 交點測試中會先測與 Voxel Bbox 交點，所以最好直接給他已轉好的 Ray(Object Space)。46,92251.9%
由於 Bbox(Point, Point) 建構時都要重新判斷 min max，改用先建構空的 Bbox 再直接給值(pmin, pmax)省去建構時間。36,76840.7%
把用不到的 Bbox 給 Voxel 交點測試中再利用，節省 Construction Time(避免重新 relocate 記憶體位置以及建構空 Bbox 的時間)。32,74236.2%
  • Intersect() 欄的數字是指 CPU 採樣時落在這函式的總樣本數，越多表示執行時間越長
  • 測試的是 landsea-2.pbrt，並且使用 –ncores 1 以減少多執行緒的誤差

經過幾次最佳化後，成功壓低執行時間(單位為秒)，效能比較如下:

效能比較。<sup>[3]</sup> 效能比較。[3]

雜談

說真的這大概是我做過數一數二難的作業了，而且竟然只是作業一….
其實寫的過程也不是我自己想到的，老師也有給提示，甚至網路上其實根本有答案….(不見得是最佳解就是了)
為了這作業我甚至還上 Stack overflow 問了人生第一個問題 哈哈(雖然問題跟演算法沒關係)
只能說不愧是 Stanford 的題目囉？

註:
[1] 可以看這篇介紹 IKEA 渲染型錄
[2] 原圖來自 Physically Based Rendering, Second Edition
[3] 執行時間用 bash 內建 time 指令來量測